Все, что я желаю — это стать настоящим журналистом,
честным и ответственным за каждое опубликованное слово.
Чарльз Доу
Чуть раньше я описал фрактальную структуру волнового движения курсов валют или акций. Согласно теории хаоса основой для появления такой структуры является многократное применение во времени однородных действий к какому-либо объекту, на картинке ниже легко увидеть множество аналогичных структур, возникающих при постепенном формировании:
— галактики, собирающиеся из космического газа и пыли
— ураганы, формирующиеся из множества ветров
— дома улиток
— кроны деревьев
— изрезанные линии побережий
— и многое другое
Движение цен на рынке тоже являются случаем многократного применения простой операции — сделки, она выполняется когда цена продажи актива какого-то продавца и цена покупки некоторого покупателя равны. В этом случае текущая стоимость актива (нефть, валюта, акция) становится равной этой цене. Следующая сделка может изменить эту цену и так далее. В итоге формируется график цены стоимости актива от времени, являющийся результатом многократных простых сделок купли-продажи. Очевидно, что в соответствии с теорией хаоса его строение будет фрактально (самоподобно) на различных временах. Следующим очевидным выводом будет соответствие характерных размеров движений вниз или вверх золотому сечению. Откуда собственно и вытекает эффективность использования чисел Фибоначчи, предел отношения которых стремится к золотому сечению.
Как известно, Леонардо Пизанский (Фибоначчи) — один из крупнейших математиков Средневековья, который изучал математику у лучших на тот момент специалистов — арабов, в Алжире и Египте, прежде всего Аль-Хорезми. Благодаря арабским переводам он познакомился и с трудами античных и индийских математиков.
Формула чисел Фибоначчи выглядит следующим образом, первые два числа 0 и 1
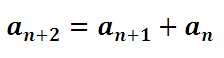
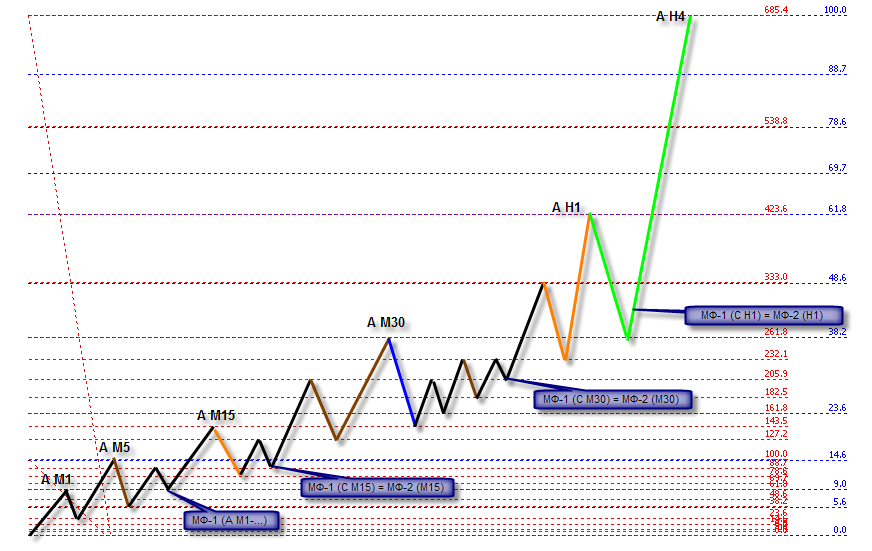
На втором рисунке показан постепенный рост характерного размера волны. Таким образом, если определить опорную (в идеале минимальную по размеру) волну, можно рассчитать цели движения стоимости актива в направлении импульса, а в совпадении этих уровней с уровнями коррекции (третий рисунок) находятся наиболее вероятные цели изменения размера волны (откат с последующим ростом).
Золотое сечение — Фрактальные фигуры в природе

Структура роста волны от меньшего характерного размера к большему
Соответствие уровней коррекционных сеток к импульсным сеткам Фибоначчи